本ブログは、これからデータ分析を学ぼうとしている方向けに、最短で動かす方法をシェアすることを目的としています。従って、動くコードに主眼をおいています。
今回扱うテーマは線形回帰モデルの評価指標である決定係数です。
決定係数は、回帰係数の仮説検定と並び、回帰分析の重要な評価指標です。
説明変数の具体的な影響の有意性とは別に、説明変数のもつ目的変数に対する説明力を数値化したものですので、分析全体の精度を確認することができます。
決定係数(寄与率)とは?高い場合と低い場合の解釈と相関との関係をわかりやすく
データ分析を進めるなかで、算出した線形回帰モデルを評価したいときがあると思います。ここでは、「社会科学のためのデータ分析」で用いられているオープンデータセットを例に説明します。
データセット1:フロリダ州の郡レベルでの1996年と2000年のアメリカ大統領選挙データ
| 変数 | 説明 |
|---|---|
| country | 郡の名前 |
| Clinton96 | 1996年のクリントンの得票数 |
| Dole96 | 1996年のドールの得票数 |
| Perot96 | 1996年のペローの得票数 |
| Bush00 | 2000年のブッシュの得票数 |
| Gore00 | 2000年のゴアの得票数 |
| Buchanan00 | 2000年のブキャナンの得票数 |
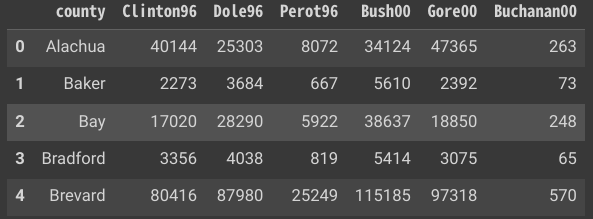
ここでは、共にリバタリアン(自由至上主義)で1996年に立候補したロス・ペロー(Ross Perot)と、彼と同じ政党から2000年に立候補したパット・ブキャナンに注目し、前者への投票から後者への投票を予測してみたい。
「社会科学のためのデータ分析入門(上)」4予測 4.2 「線形回帰」
本書では、以下の順番で線形回帰モデルの作成・ブラッシュアップと評価を行っています。
- 線形回帰モデルを作成し、決定係数を使用してモデルを評価
- 詳細を調査し、外れ値を探す
- 外れ値を取り除いて線形回帰モデルを作成し、再度評価
下記散布図(図1)は、2. で外れ値を探すために使用した残差プロットになります。
右上に予測誤差が大きな外れ値(パームビーチ郡)が存在することが解ります。
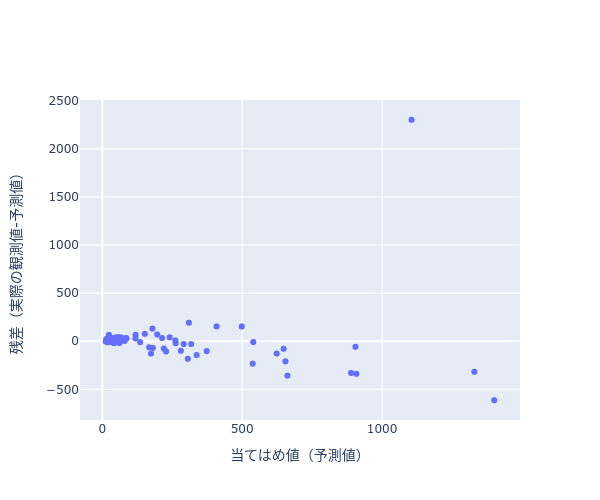
外れ値を取り除いた結果、以下が読み取れます。
パームビーチ郡を除くと、決定係数はそれまでの0.51から0.85へと劇的に向上した。モデルの当てはまりの改善は、残差プロットや回帰直線を伴った散布図からも簡単に見て取れる。
「社会科学のためのデータ分析入門(上)」4予測 4.2 「線形回帰」
このように、決定係数を導入することで、手っ取り早くモデルの評価が出来ます。
本記事では、Pandas の DataFrame と目的変数を表すカラム名と説明変数を表すカラム名の配列をインプット情報として、線形回帰を実施した後、決定係数を算出するメソッド(動くコード)を紹介します。
線形回帰と決定係数の算出を行うサンプルコード
(Colab で利用可能)
下記コードを Google Colaboratory のセルにコピペして実行することで直ぐに使えます。
メソッド①:線形回帰と決定係数を算出する
import numpy as np
from sklearn.linear_model import LinearRegression
def pyR2(_df, _x:list, _y):
_X = _df[_x].values
_Y = _df[_y].values
lr = LinearRegression()
# 線形モデルの重みを学習
lr.fit(_X, _Y)
# 予測値
Y_pred = lr.predict(_X)
# 実際の値
Y_test = _Y
# SSR=残差平方和
Err = Y_test - Y_pred
SSR = np.dot(Err, Err)
# 総平方和
_Y_float = _Y.astype(np.float64)
_Y_diff_mean = _Y_float- st_Mean(_Y_float)
TSS = np.dot(_Y_diff_mean, _Y_diff_mean)
R2 = (TSS-SSR)/TSS
print('intercept = ', lr.intercept_) # 切片を出力
print('coefficient = ', lr.coef_) # 説明変数の係数を出力
print(f"決定係数 = {R2}")
return lrメソッド①の使用例
import pandas as pd
# フロリダ州の郡レベルでの1996年と2000年のアメリカ大統領選挙データ
df_florida = pd.read_csv("https://raw.githubusercontent.com/kosukeimai/qss/master/PREDICTION/florida.csv")
# 1996年に立候補したロス・ペロー(Ross Perot)と、
# 彼と同じ政党から2000年に立候補したパット・ブキャナンに注目し、
# 前者への投票から後者への投票を予測、決定係数を算出
pyR2(df_florida, ["Perot96"], 'Buchanan00')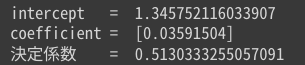
メソッド②:線形回帰を行って予測値と差異をプロットする
def plot_pred_Err(_df, _x:list, _y):
_X = _df[_x].values
_Y = _df[_y].values
lr = LinearRegression()
# 線形モデルの重みを学習
lr.fit(_X, _Y)
# 予測値
Y_pred = lr.predict(_X)
Err = _Y - Y_pred
fig = go.Figure(
data=go.Scatter(
x=Y_pred,
y=Err,
mode='markers'
)
)
fig.update_layout(
width=600,
height=500
)
fig.update_xaxes(
title_text="当てはめ値(予測値)",
)
fig.update_yaxes(
title_text="残差(実際の観測値-予測値)"
)
fig.show()
_df["Err"] = pd.DataFrame(Err)
return _dfメソッド②の使用例(1):可視化
import pandas as pd
# フロリダ州の郡レベルでの1996年と2000年のアメリカ大統領選挙データ
df_florida = pd.read_csv("https://raw.githubusercontent.com/kosukeimai/qss/master/PREDICTION/florida.csv")
df_florida_2 = plot_pred_Err(df_florida,["Perot96"],"Buchanan00")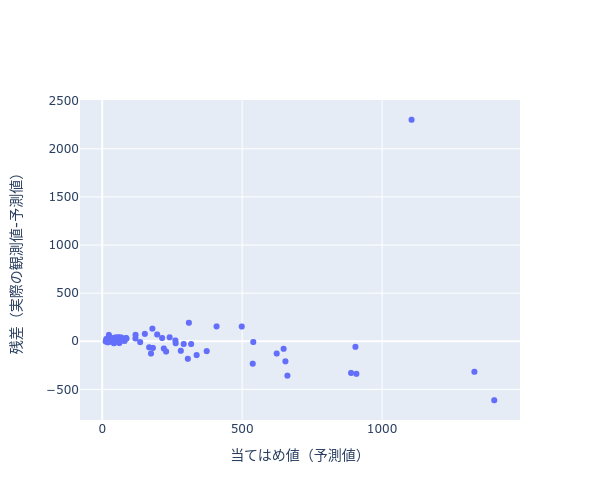
メソッド②の使用例(2):外れ値の抽出と外れ値を除いての線形回帰
図1の右上の外れ値を抽出します。残差が最大のレコードを抽出します。
# 異常値を抽出
df_florida_2[df_florida_2["Err"]==df_florida_2["Err"].max()]
パームビーチ郡が外れ値であることが解りました。
パームビーチ郡を除いて線形回帰を行って、決定係数を算出します。
# 異常値を除いた決定係数
pyR2(df_florida_2[df_florida_2["county"]!="PalmBeach"], ["Perot96"], 'Buchanan00')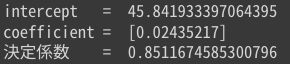
外れ値(パームビーチ郡)を除くことで、決定係数が0.51から0.85に良化したことが解ります。
まとめ
本記事では、Pandas の DataFrame と目的変数を表すカラム名と説明変数を表すカラム名の配列をインプット情報として、線形回帰を実施した後、決定係数を算出するメソッドを紹介しました。
ご参考になりましたら twitter をフォローして SNS でシェアして頂ければ幸いです。
また、データのビジュアル化に興味のある方は合わせて下記もご参考ください。
また、データ分析に関して、一つ一つ丁寧に確認したい方は下記記事をご覧ください。